Продолжение заметки о визуальных атомах. Сегодня поговорим о прямоугольниках, отрезках и линиях.

Прямоугольник
Прямоугольники обладают четырьмя собственными свойствами (ширина, высота, их производная — площадь, цвет) и легко складываются друг с другом.

Прямоугольники единичной ширны складываются в столбиковую диаграмму:

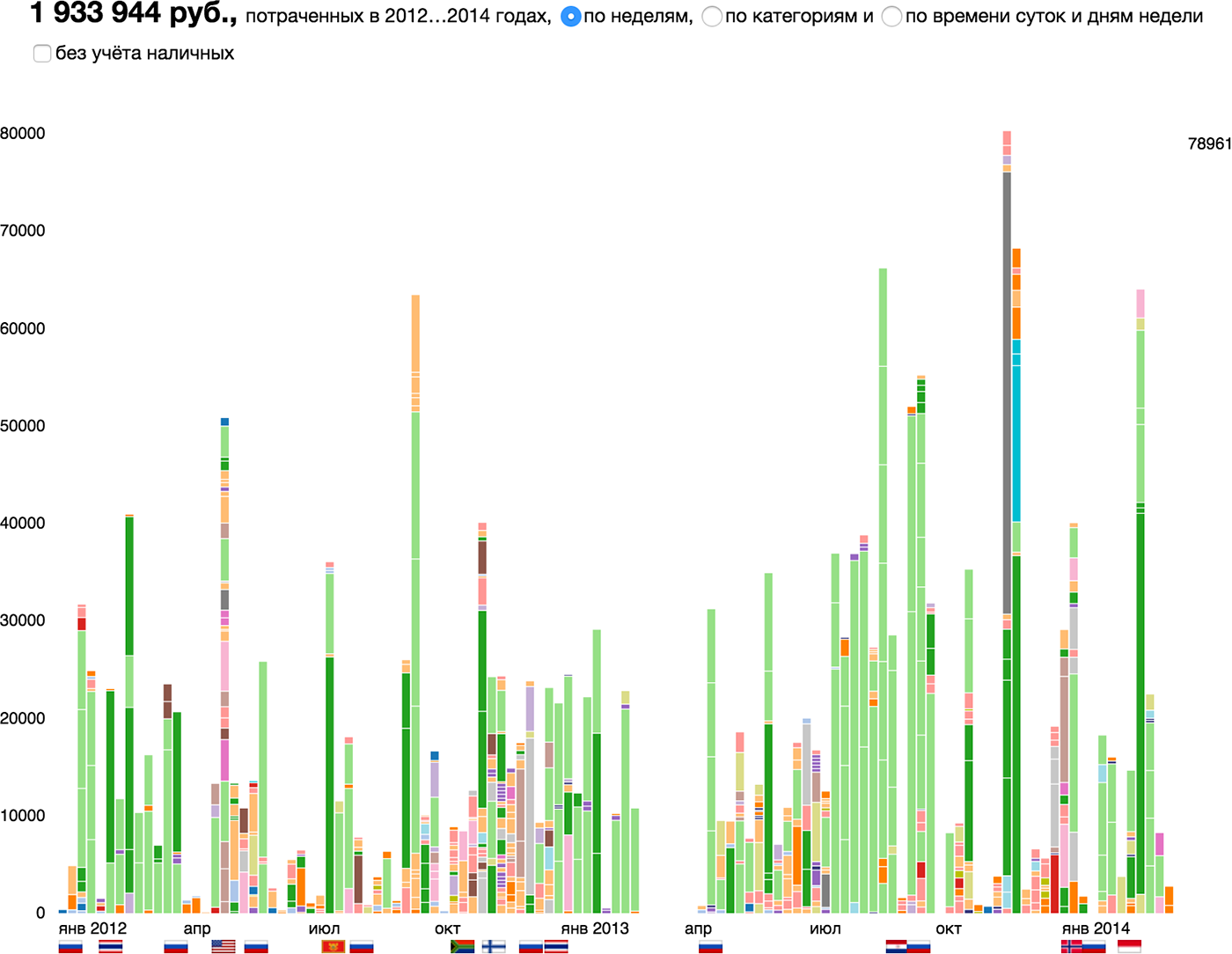
Элементарная частица в личных финансах — трата, визуальный атом — прямоугольник единичной ширины, его высота соответствует размеру траты, цвет — категории. На диаграмме траты суммируются, высота столбика показывает размер недельных трат.

Элементарная частица продаж интернет-магазина — продажа, визуальный атом — прямоугольник единичной ширины, его высота соответствует сумме продажи. Высота столбика на диаграмме показывает суточную выручку. Цветом показаны будни и выходные дни.

Прямоугольники подходят для отображения групп элементов (чаще неразличимых пикселей, редко — точек), в этом случае ширина и высота прямоугольника задействуются для визуализации параметров группы. Важно выбирать параметры для ширины и высоты так, чтобы их произведение — площадь, также имело физический смысл.

Например, если количество детей в возрастной группе задаёт высоту прямоугольника, а доступность садиков для этой группы — его ширину, то площадь прямоугольника соответсвует количеству детей этого возраста, попавшему в сад.

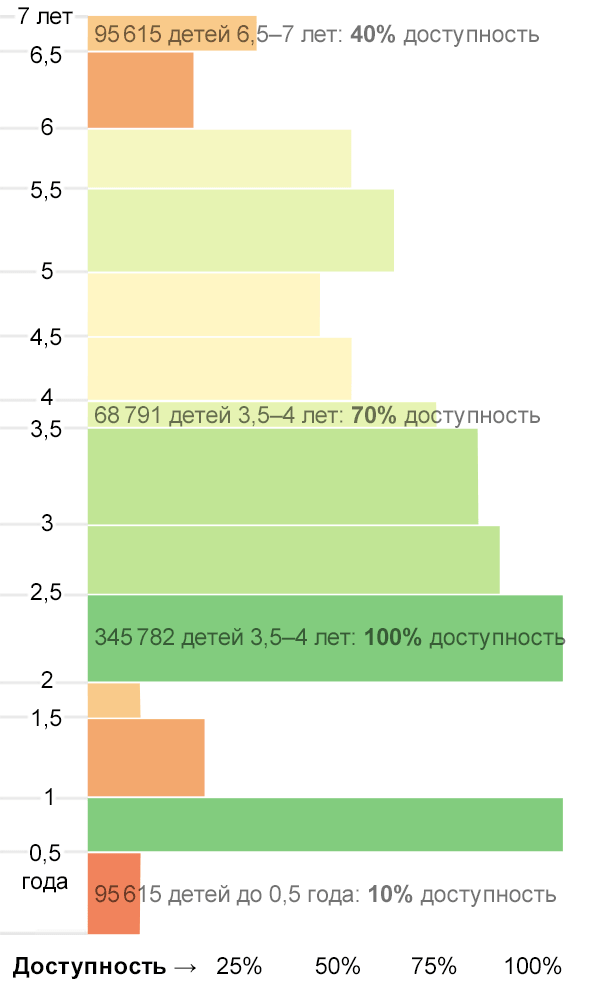
Видим, что проблема для группы 1,5-2 года стоит острее, чем для группы 2-2,5 года — хоть доступность садов в ней и выше, но нуждающихся в садике детей намного больше.

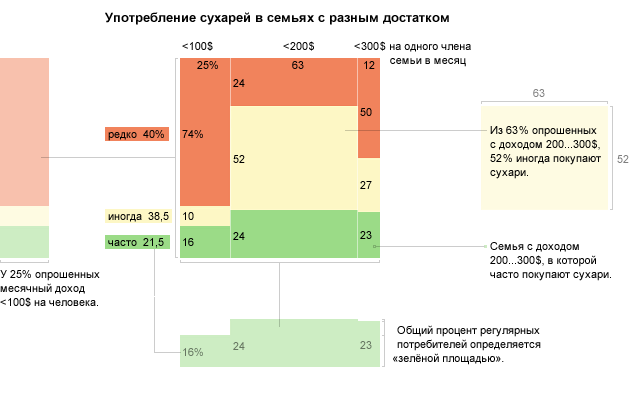
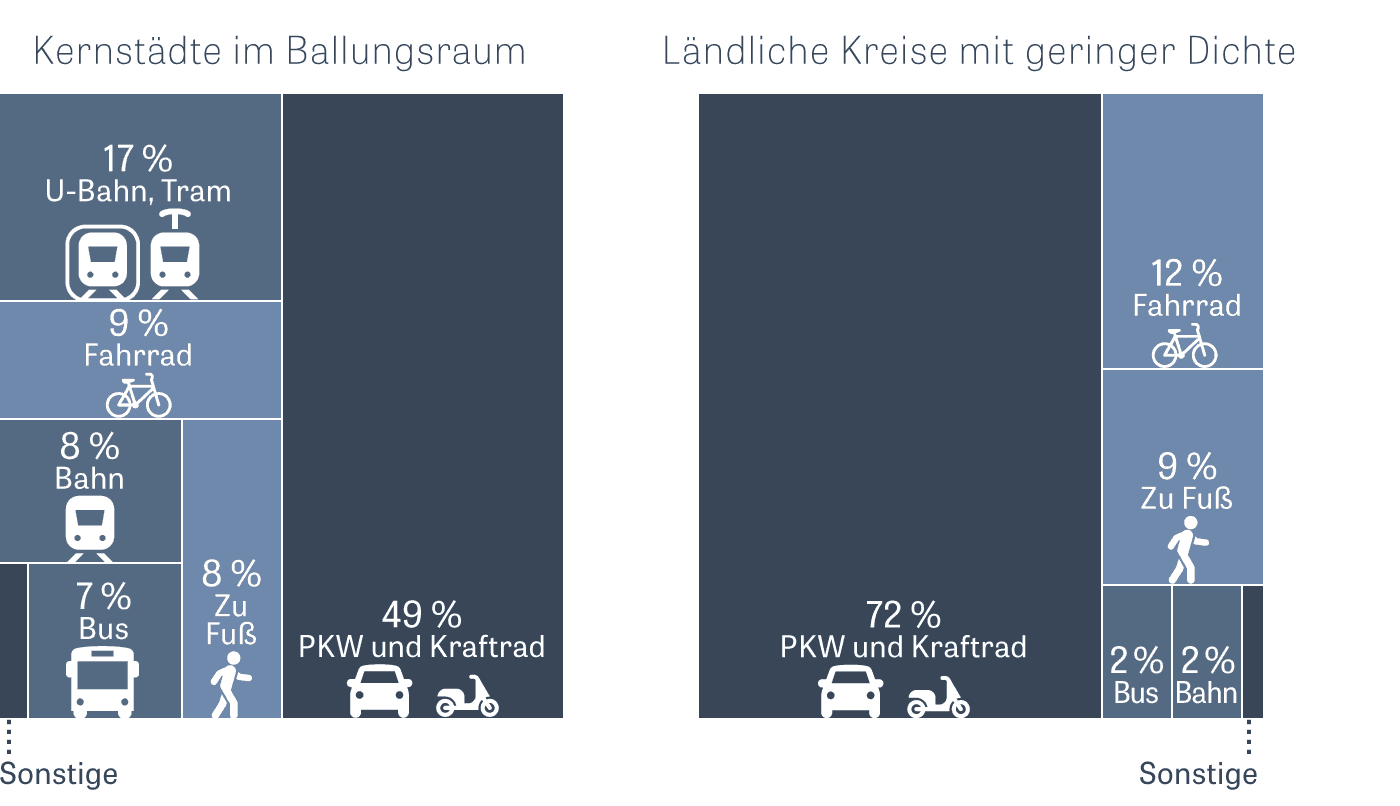
По такому же принципу прямоугольники образуют квадратные и тримэп-диаграммы:

Отрезок
Отрезок визуализирует частицу данных, состоящую из двух связанных элементов.

Это может быть связь двух объектов, например, брачный союз людей разных профессий:

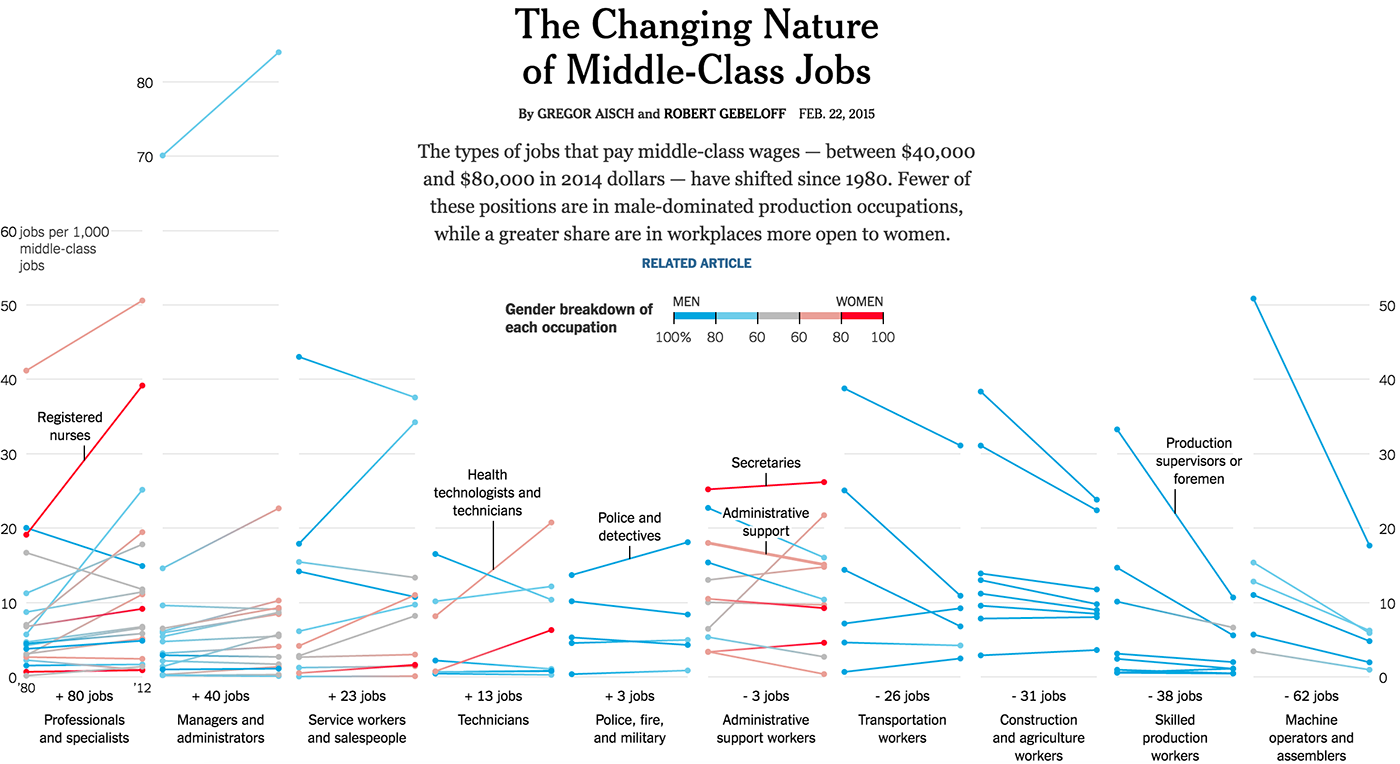
Связь «до и после» двух значений одного и того же параметра, например, количество высокооплачиваемых должностей в различных индустриях:

.
Связанные попарно значения, например, результаты ответов на вопросы теста, личный и средний по соотечественникам:

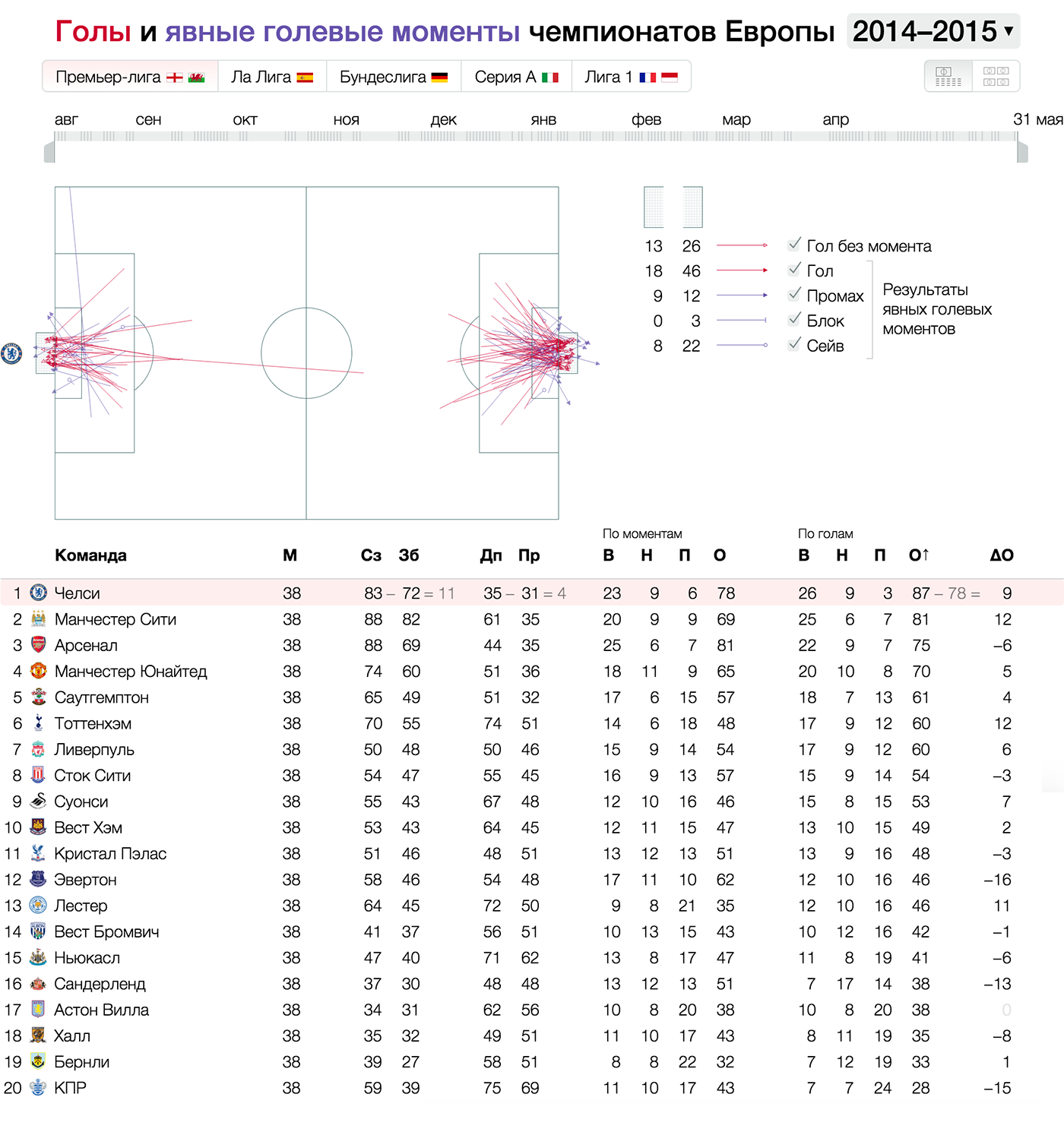
Или пара связанных пространственных координат, например, начальное и конечное положение мяча при ударе по воротам:

Линия
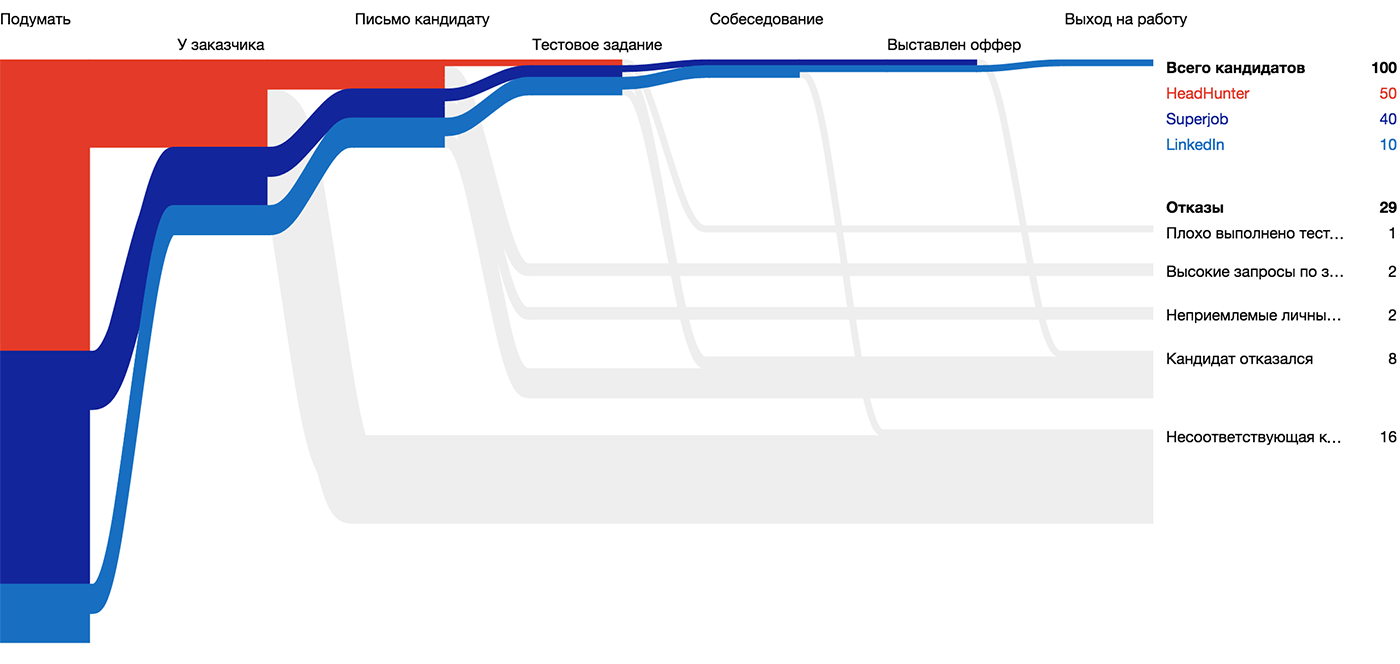
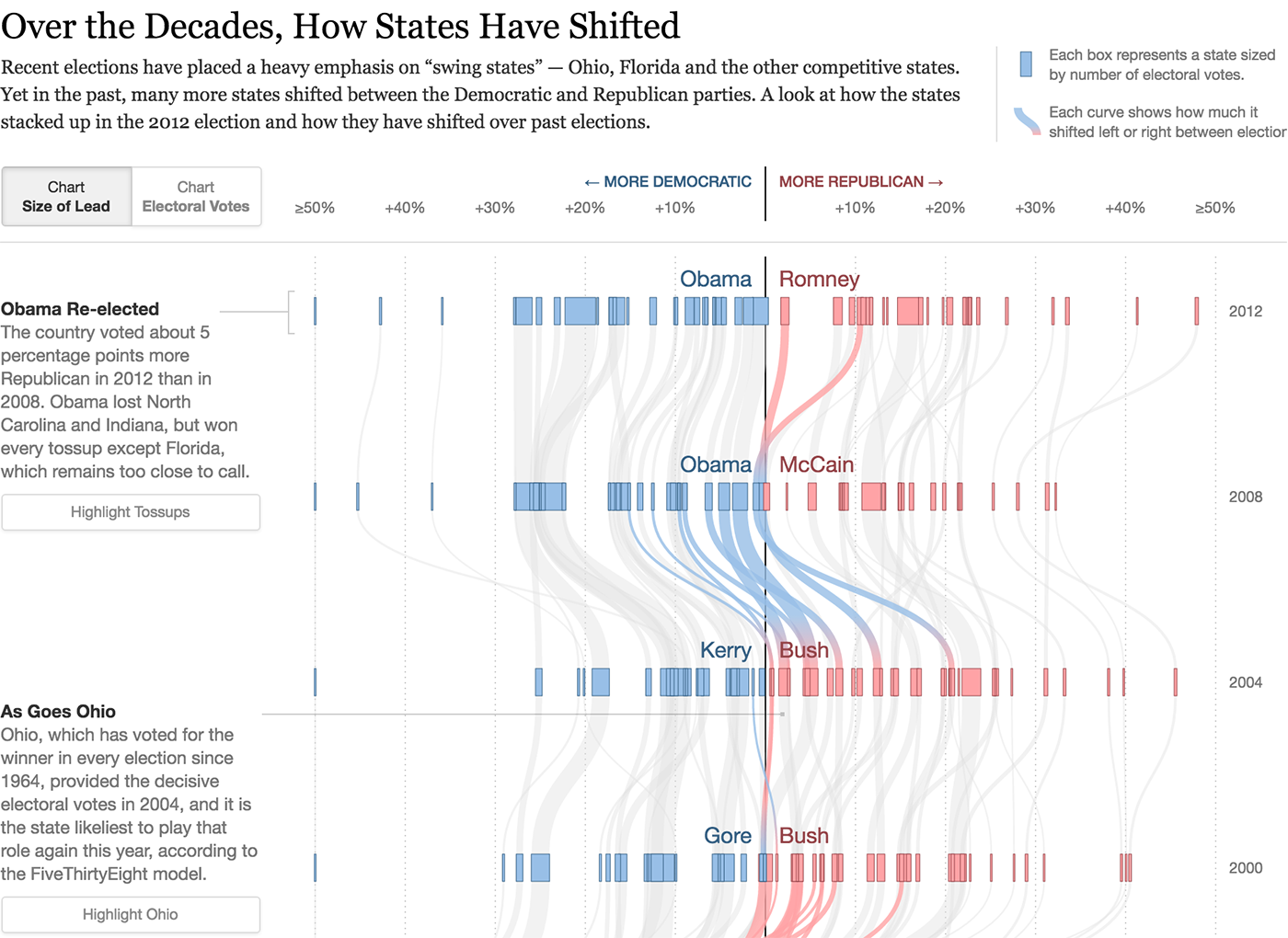
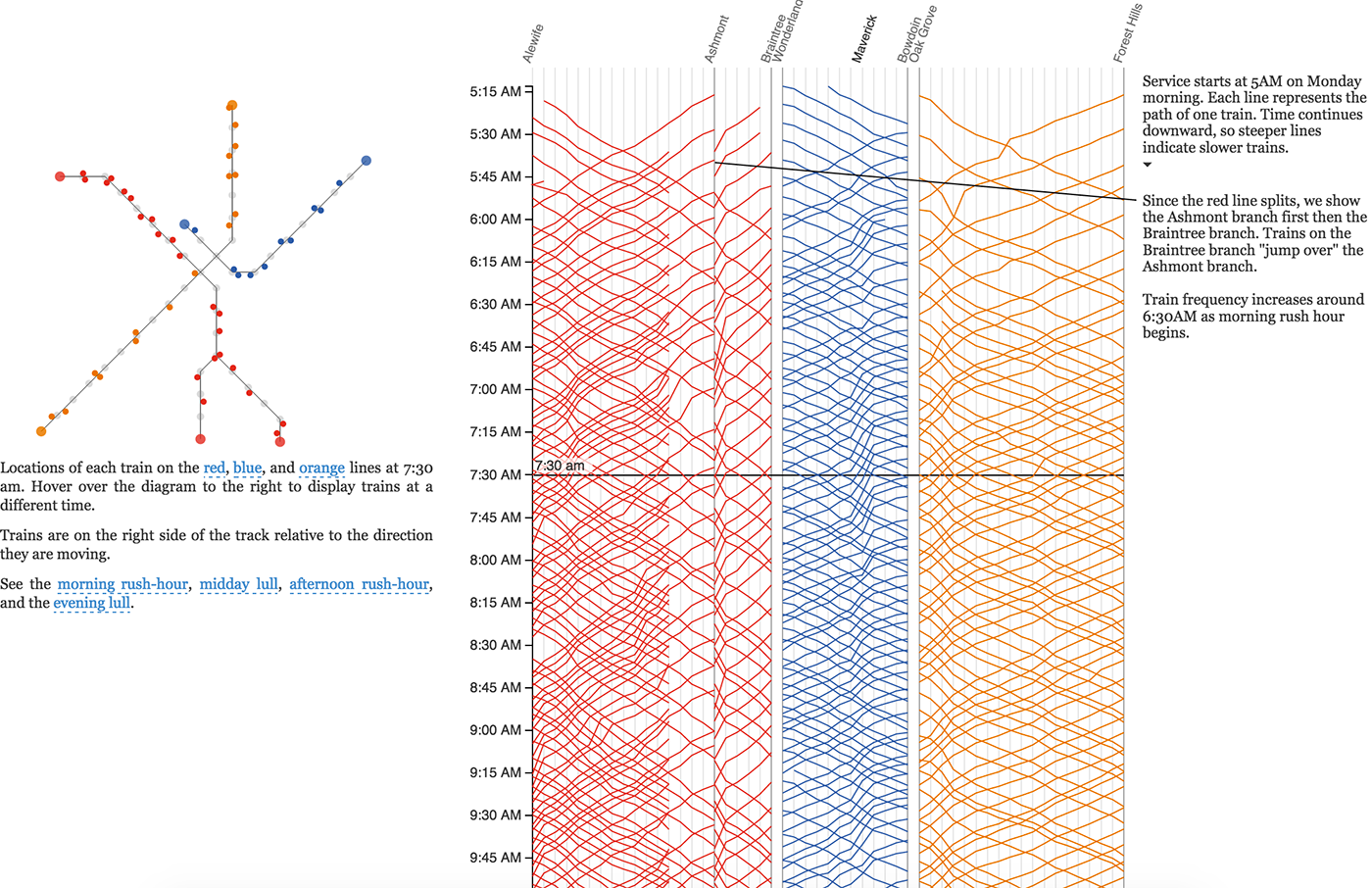
Линия показывает путь или историю объекта во времени. Для линии важны не только точка начала, точка конца и связь (как в отрезке), но и форма пути между ними. Линии сливаются в потоки и делятся на русла.

Частица данных — кандидат, проходящий этапы воронки собеседований

Частица данных — штат, изменяющий свои настроения во времени

Частица данных — поезд метро, движущийся между станциями

Частица данных — заключённый, проводящий срок в тюрьме Гуантанамо

Частным случаем линии является географический маршрут.

Частицы данных — французы армии Наполеона, наступающие на Москву и отступающие обратно

О мини-графике и географических атомах (точке, области, объекте и маршруте) я расскажу в третьей, заключительной заметке.

Следующая теоретическая заметка выйдет 4 июля.